Mi investigación se centra en derivar y analizar teórica y numéricamente nuevos modelos matemáticos que describan diferentes procesos multiescala en mecánica de fluidos.
El estudio del comportamiento de los fluidos es esencial para comprender diversos fenómenos en la ingeniería y las aplicaciones a otras ciencias, ya que arroja luz sobre el complejo movimiento y las interacciones de líquidos y gases. Mi investigación se centra en el estudio de diferentes tipos de fluidos:
El modelado de flujos de fluidos no newtonianos en dominios complejos (como dominios delgados, dominios porosos, dominios rugosos, dominios delgados porosos o dominios delgados rugosos) es fundamental debido a sus aplicaciones prácticas, por ejemplo, en el procesamiento de polímeros, en el transporte de petróleo en tuberías, en hidrología, así como el procesamiento de alimentos.

Dominios delgados porosos
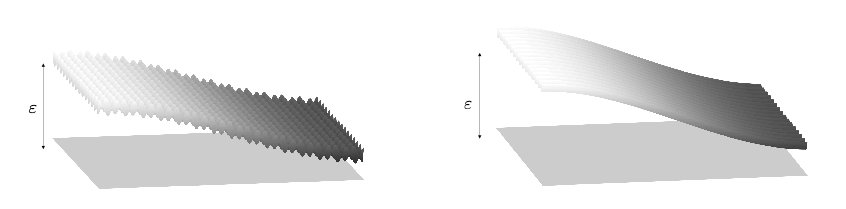
Dominios delgados rugosos
Las ecuaciones que gobiernan los fluidos que estudio son demasiado complejas para resolverse en tales dominios debido a su compleja geometría. Mi investigación se centra en la derivación de leyes macroscópicas planteadas en dominios más simples, conteniendo cantidades promediadas que reflejen las heterogeneidades de los dominios, que sustituyan las leyes físicas originales y nos permitan conocer su comportamiento de manera aproximada. Para conseguir este tipo de ecuaciones promediadas mejoro y uso técnicas recientes de la Teoría de la Homogeneización.
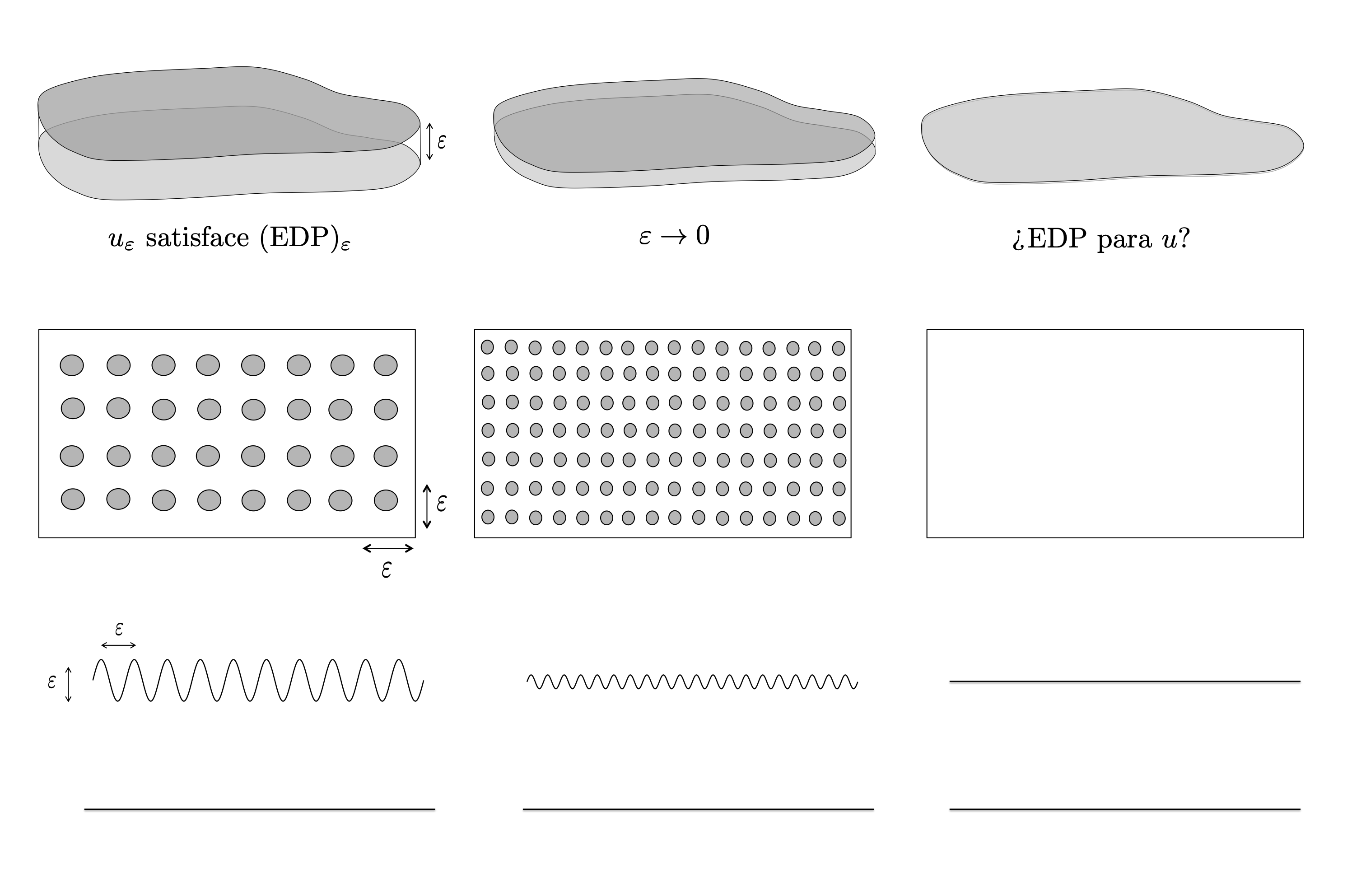
Proceso de homogeneización en dominios delgado, poroso y rugoso
Una vez obtenidos los modelos macroscópicos, hay que proceder a su verificación. Los métodos numéricos usuales pueden resultar computacionalmente muy costosos para resolver los problemas originales planteados debido a la complejidad de las estructuras de los dominios, sin embargo, el uso de los modelos macroscópicos obtenidos permite reducir drásticamente el coste computacional en su resolución numérica. Con el fin de validar y comparar los distintos modelos que se obtengan, realizo simulaciones numéricas, mejorando algoritmos basados en el Método de Elementos Finitos, por ejemplo, usando el software FreeFem++.